| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 독서노트
- Leet Coding Challenge
- leet code
- 전자공학
- 신호처리
- DTFT
- 코테준비
- 이산신호처리
- 알고리즘문제풀이
- 알고리즘
- 컨볼루션
- leetcode
- PYTHON
- 카카오 코딩테스트
- 코테
- 백준
- IOS
- DSP
- 프로그래머스
- backjoon
- 코딩테스트
- SWIFT
- dft
- SWIFTUI
- 파이썬
- 스위프트
- Trie
- 릿코드
- 알고리즘 문제풀이
- 트라이
- Today
- Total
목록디지털신호처리, DSP (12)
매일 매일 성장하는 섭섭군
 [Seop's 강의노트] MATLAB에서 Convolution 함수 구현
[Seop's 강의노트] MATLAB에서 Convolution 함수 구현
저번학기에 이산신호에 관하여 배우면서 포스팅을 진행 하였지만 MATLAB을 사용하여 실습은 진행하지 않았다. 이번학기에 신호처리 실습을 배우는 만큰 어떻게 구현하는지에 대하여 글을 써보고자 한다. 신호처리와 관련해서 가장 먼저 한 실습은 컨볼루션과 관련된 실습이다. 신호처리 과목에서 컨볼루션은 가장 기본이 되는 만큼 가장 처음으로 진행한 것 같다. MATLAB 코드와 함께 설명하는 방식으로 포스팅을 진행할 예정이다. 다만 코드인 만큼 주관적인 생각이 강하고 아직 필자가 MATLAB을 배우고 있는 초보적인 수준이라 잘 짠 코드라고는 말하기 힘들 것 같다. 본론으로 돌아가 Convolution 함수를 구현을 실행해 보자 컨볼루션 함수는 메틀랩에서 제공해 준다. conv(x,h) 를 사용하면 된다. 하지만 우..
 [Seop's 강의노트] 이산신호처리 _ DFT, Zero Padding
[Seop's 강의노트] 이산신호처리 _ DFT, Zero Padding
이번 포스팅에서는 DFT의 대해서 좀 더 잘 알아보고자 한다. DFT는 DTFT를 통해서 나온 신호가 0~2pi 주기로 연속이었다. 연속이기 때문에 신호처리가 쉽지 않아 Sampling 한것처럼 다시 쪼갠 것이다. 예시를 같이 봄으로서 이해해 보도록 하자. 이산 신호 x[n]을 DTFT 변환을 한 결과이다. 다음과 같이 2pi 마다 반복하는 연속적인신호가 나오게 된다. 그런데 식을 잘 살펴보면 x[n]에서 앞에 있는 두 1의 값은 DTFT에 영향을 미치지만 뒤에 있는 0은 값들은 영향을 미치지 않는다. 그렇다면 왜 굳이 있는 것일까? 일단 한번 임의의 N개로 나누어보았다. 0번부터 시작해서 N-1 까지 이루어져 있다. 여기서 한가지 알고 가야 할 개념이 있다. 바로 분해능(Resolution) 이라는 것..
 [Seop's 강의노트] 이산신호처리 _ DFT의 개념
[Seop's 강의노트] 이산신호처리 _ DFT의 개념
지금우리는 신호처리에 관하여 공부하고 있다. 연속 신호인지? 주기성이 있는지? 시간 도매인 인지? 주파수 도매인인지 등 여러가지를 배웠다. 이런 많은 것들을 배우는 목적은 아날로그 신호를 디지털화 시켜서 컨트롤 하고 새로운 신호를 만들어내 이것을 전송하며 아날로그화 시키려고 하는 것이 목적이다. 자연속에 존재하는 연속 비주기 신호에 대한 정보를 알기 위해서 CTFT 란 것을 배웠으며 이를 우리가 컨트롤 하고 싶어서 표본화 과정을 거쳐 이산신호로 만들었다. 이렇게 만든 이산신호의 주파수 정보를 알아보기 위해 DTFT란 것을 배웠다 그런데 문제가 하나 생겨버렸다. 연속 비주기 신호를 표본화 시켜서 얻어낸이산신호에 대한 주파수 정보들이 연속이 되어 버렸다. 연속이란 의미는 수없이도 많은 정보를 가지고 있다고 ..
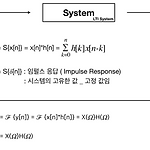 [Seop's의 강의노트] LTI 시스템, 컨벌루션 이란?
[Seop's의 강의노트] LTI 시스템, 컨벌루션 이란?
저번 포시팅 때 DTFT의 특징 및 성질의 관하여 알아보았다. 오늘은 그 성질들 중에서 컨벌루션(convolution)에 관한 것을 알아볼까 한다. 일단 convolution 의 뜻이 뭘까? 사전적 의미로는 서로 얽혀 있는 것, 돌돌 말려있는 것 이라고 해석 할 수 있다. 이를 우리가 지금 공부하고 있는 신호로 가져와서 해석한다면 신호들이 서로 얽혀있는것 , 말려있는 것 이라고 생각해 볼 수 있다. 위의 식들을 한번 살펴보자면 입력신호x[n]과 임펄스 응답 신호 h[n]이 서로 영향을 주어서 출력신호 y[n]이 나오게 된다. System을 자세히 한번 들여다보면 LTI 시스템이라고 써져있다. 컨벌루션이 가능하려면 LTI 시스템이여야 한다고 한다. 그렇다면 LTI 시스템이란 무엇일까? LTI (Linear..
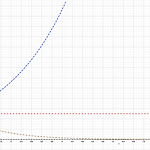 [Seop's 강의노트] 이산신호처리 _ DTFT의 특징 및 성질
[Seop's 강의노트] 이산신호처리 _ DTFT의 특징 및 성질
지금 우리는 푸리에 분석에 관하여 배우고 있다. 지금까지 배웠던 것을 간단히 정리해 보자면 다음과 같다. CTFS - 연속 시간 푸리에 급수 _ 연속 주기신호 V T(주기)를 무한대로 보낸다. V CTFT - 연속 시간 푸리에 변환 _ 연속 비주기 신호 V 표본화(Sampling) V DTFT- 이산 시간 푸리에 변화 _ 이산 비주기 신호 이러한 과정을 거쳐서 현재 DTFT에 관하여 공부하고 있다. 오늘은 DTFT의 특징 및 성질에 관하여 알아보고자 한다. DTFT 의 가장 큰 특징은 두가지로 볼 수 있다. 1. 반복성 , 주기성을 가진다. 저번 포스팅에서도 설명이 되어있듯이 2파이 마다 반복하는 것을 알 수 있다. 2. 모든 오메가(주파수)에 대해 스펙트럼이 존재한다. 즉 오메가에 대해서 연속이다. -..
 [Seop's 강의노트] 이산신호처리 _ 표본화(Sampling)
[Seop's 강의노트] 이산신호처리 _ 표본화(Sampling)
저번 시간에는 DTFT에 관한 것들을 알아보았다. 오늘은 저번 시간에 이어서 DTFT에 관련된 표본화에 대해서 배워볼까 한다. 표본화란 무엇일까? 기억이 날지 모르겠지만 우리는 이미 표본이라는 단어를 들은 적이 있다. 고등학교 시절 통계를 배울때 표본추출 이라는 단어가 나왔을 것이다. 즉 원래의 집단에서 일부분을 뽑아내는 것을 표본화 라고 한다. 그러면 우리가 배우고 있는 신호에서 표본화란 무엇일까? 통계때랑 비슷하다 대신 우리는 일정한 주파수를 설정한 후에 뽑아낸다. 표본화 할때 쓰는 주파수를 표본화 주파수(fs)라고 하며 정의는 다음과 같다. 표본화 주파수(fs) : 1초동안 몇회 표본화 하는가에 대한것. 즉 원신호를 1초동안에 10번을 뽑아낼 것인지 1,000번을 뽑아낼 것이지 하는 것이다. 다음 ..
 [Seop's 강의노트] 이산신호처리 _ DTFT, 이산시간 푸리에 변환
[Seop's 강의노트] 이산신호처리 _ DTFT, 이산시간 푸리에 변환
지금 우리는 ‘푸리에 분석’이라는 도구에 관해서 배우고 있다. 지금까지 연속 주기 신호, 연속 비주기 신호 를 분석하는 CTFS, CTFT를 알아보았다. 이산 비주기 신호에 관하여 알아보도록 하자. 이산 비주기 신호는 연속 비주기 신호를 표본화(Sampling) 하여서 얻어낸 것이다. 표본화 과정은 다음 포스팅때 자세하게 배우겠지만 간단하게 설명해보자면 연속 비주기시 신호 (아날로그 신호)에서 일정 간격으로 주파수 성분과 크기를 뽑아내는 것이다. 흔히 통계에서 전체집단 중 일부를 뽑아내는 것과 같은 개념이라고 볼 수 있다. 그렇다면 연속 비주기 신호를 표본화 하여서 이산 비주기 신호를 얻어냈다면 어떠한 변화가 있을까? 연속 비주기 신호를 샘플링 한 후의 변화이다. 여기서 지켜봐야 할 특징은 시간의 개념이..
 [Seop's 강의노트] 이산신호처리 _ CTFT, 연속시간 푸리에 변환
[Seop's 강의노트] 이산신호처리 _ CTFT, 연속시간 푸리에 변환
지금우리는 푸리에 분석 이라는 툴에 대해서 배우고있다. 푸리에 분석의 목적은 신호에 어떤 주파수 성분이 들어있는지? 또 얼만큼씩 들어있는지? 를 알아보는 것이다. 처음 으로 CTFS _ 연속시간 푸리에 급수에 관해서 배웠다. 이는 연속주기신호 xp(t)에 관해서 푸리에 분석을 해본 것이었다. 자세한 사항은 링크를 참조해보면 알 수 있을 것이다. https://richard25.tistory.com/6 [Seop's 강의노트] 이산신호처리 _ CTFS 연속시간 푸리에급수. 오늘은 푸리에 분석 중에서 CTFS에 관련해서 알아보도록 하자. CTFS(Continuous Time Fourier Series) 를 한국어로 번역해 보자면 ‘연속시간 푸리에 급수’ 이다. CTFS는 연속주기신호를 대상으로 만들.. ri..
