| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- leet code
- 알고리즘문제풀이
- PYTHON
- 코테
- 백준
- DTFT
- 전자공학
- Trie
- 독서노트
- Leet Coding Challenge
- 카카오 코딩테스트
- SWIFT
- 코테준비
- DSP
- 파이썬
- backjoon
- 신호처리
- 프로그래머스
- 릿코드
- dft
- 트라이
- 코딩테스트
- SWIFTUI
- 알고리즘 문제풀이
- leetcode
- 스위프트
- 컨볼루션
- 이산신호처리
- 알고리즘
- IOS
- Today
- Total
매일 매일 성장하는 섭섭군
[Seop's 강의노트] 이산신호처리 _ DFT, Zero Padding 본문
이번 포스팅에서는 DFT의 대해서 좀 더 잘 알아보고자 한다.
DFT는 DTFT를 통해서 나온 신호가 0~2pi 주기로 연속이었다.
연속이기 때문에 신호처리가 쉽지 않아 Sampling 한것처럼 다시 쪼갠 것이다.
예시를 같이 봄으로서 이해해 보도록 하자.

이산 신호 x[n]을 DTFT 변환을 한 결과이다. 다음과 같이 2pi 마다 반복하는 연속적인신호가 나오게 된다.
그런데 식을 잘 살펴보면 x[n]에서 앞에 있는 두 1의 값은 DTFT에 영향을 미치지만
뒤에 있는 0은 값들은 영향을 미치지 않는다. 그렇다면 왜 굳이 있는 것일까?

일단 한번 임의의 N개로 나누어보았다.
0번부터 시작해서 N-1 까지 이루어져 있다.
여기서 한가지 알고 가야 할 개념이 있다.
바로 분해능(Resolution) 이라는 것이다.
분해능을 이해하기 쉽게 말하자면 모니터 해상도 같은 개념이다.
우리가 UHD,FHD등으로 선명한 화질의 TV나 모니터를 이야기 한다.
UHD는 3840x2160 의 해상도를 FHD는 1920x1080의 해상도를 가진다.
즉 같은 크기의 화면일때 하나의 빛을 나타내는
점을 얼마나 촘촘하게 나누었는지에 대한 의미이다.
위 신호에서는 점과 점 사이의 거리를 분해능이라고 하는데
그 길이가 짦을수록 분해능이 좋다는 의미이다.
이제 분해능 이라는 개념을 알고 다시한번 신호들을 바라봐 보자
x[n]은 4개의 신호를 가지고 있다.
즉 입력 Sample 의 개수가 4개인 것이다.
반면 내가 예시로 든 X(K)는 8개의 점을 가지고 있다.
즉 Sample의 개수가 8개라는 의미이다.
몇개로 나누었는지를 N 이라 말하고 N개로 나눈 DTFT 를.
N-Point DFT 라고 한다.
식으로 표현하자면 다음과 같다.

우리가 이해한 것으로 N 이 커지면 커질수록 분해능이 좋아진다고 한다.
그러면 이제 왜 x[n] = {1,1} 이라는 식 대신에 x[n]={1,1,0,0} 이라고 표현했는지 알아 볼 수 있다. 즉 임의로 N의 갯수를 늘려준 것이다.
많이 나누어 줌으로 인해서 분해능을 높이고 원신호에 가까워 지도록 한 것이다.
이와 같이 ‘0’을 추가로 입력하여 N의 개수를 증가시켜 주는 것을
Zero Padding 이라고 한다.
Zero Padding 의 목적은 DTFT와 가까운 DFT 를 만드는 것이다.
즉 많이 할수록 DTFT와 근접해진다.
그렇다면 무작정 Zero Padding을 많이 하는 것이 좋을까?
유한한 신호일 경우에는 많이하면 할 수록 DTFT와 근접해지는 것이 맞다. 하지만 유한하지 않은 신호에 대해서
과도한 Zero Padding 을 했을 경우에는 오차가 더 발생 할 수 있다.
Zero Padding 과는 반대의 경우도 있을 것이다.
x[n] = a^n 이라는 신호가 있다고 하자. (0<a<1)
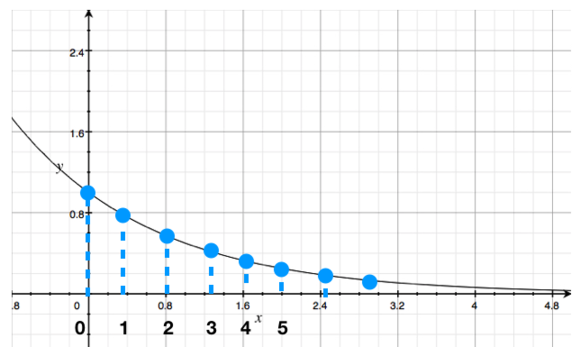
입력 샘플링 수가 9개이다. 하지만 나는 0부터 4까지의 값만 필요하고
나머지 뒤의 값은 필요하지 않는다.
이럴때 Zero Padding 과는 반대로
나머지 샘플들을 버리는 것을 Truncation 이라고 한다.
Truncation 을 과도하게 사용하게되면 DTFT의 모양을 많이 잃을 수 있기때문에 적당히 사용하여야 한다.
우리가 지금까지 무엇을 위해서 DTFT를 했으며 또 DFT를 했는가?
기억을 되짚어보면 우리는 W(오메가) 즉 연속 비주기 신호의 주파수를 알기 위해서 이 여정을 펼쳐왔다.
지금까지 배운 주파수 관련된 식을 사용해보면 다음과 같은 식을 찾아낼 수 있다.
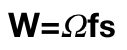
자 이제 이 식을 어디에 집어넣으면 될까? 저번 포스팅과 이번 포스팅에서 배운 DFT 를 통해서 나온것에 대입시키면 된다.
다음 그림을 보면서 이해해 보자.

x[n]={1,1,0,0,0,0,0,0,} 을 8-Point DFT 한 결과이다.
DTFT는 2파이를 주기로 갖는 주기적인 신호이고 DFT는 2파이를 N개로
나눈 것이다. 그래서 위 그림과 같은 결과가 나온다.
이로서 우리는 주파수 영역에서의 이산 값을 얻어내었다.
이를 W에 맞게 변환해 주어야 하는데 위 식을 통하면 W 값을 구할 수 있다.
지금 시점쯤에 우리가 무엇을 공부했는지 한번 뒤짚어 보자.

우리는 지금 신호에 대해서 공부하고 있다.
자연속에 존재하는 아날로그 신호인 x(t) 연속 비주기 신호의 주파수를
알기 위해서 샘플링을 하였다. 그래서 우리는 x(t) 를 잘개 쪼갠 x[n] 이라는 이산 비주기 신호를 얻어 낼 수 있었다.
x[n] 의 주파수를 알아보기 위해서 DTFT를 거치었더니 연속이라 DFT를 통해서 X[K] 를 얻어내었다.
X[K]를 통해서 우리는 x(t) 의 주파수 성분들을 알아 볼 수 있었다.
우리가 배운 것들이 다 따로따로 떨어져 있는 것들이 아니라 하나의 목적을위해서 연결된 것이라 생각하면서 신호처리를 배우는 것이
엔지니어로서 올바른 자세인 것 같다.
'디지털신호처리, DSP' 카테고리의 다른 글
| [Seop's 강의노트] MATLAB에서 Convolution 함수 구현 (0) | 2019.10.23 |
|---|---|
| [Seop's 강의노트] 이산신호처리 _ DFT의 개념 (0) | 2019.10.23 |
| [Seop's의 강의노트] LTI 시스템, 컨벌루션 이란? (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ DTFT의 특징 및 성질 (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ 표본화(Sampling) (0) | 2019.10.23 |




