| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 신호처리
- SWIFTUI
- 릿코드
- 이산신호처리
- 백준
- 독서노트
- 코테
- Leet Coding Challenge
- SWIFT
- DSP
- Trie
- 컨볼루션
- 전자공학
- backjoon
- 코테준비
- 프로그래머스
- PYTHON
- 파이썬
- 카카오 코딩테스트
- 코딩테스트
- leetcode
- 알고리즘문제풀이
- leet code
- IOS
- 트라이
- dft
- DTFT
- 알고리즘
- 스위프트
- 알고리즘 문제풀이
- Today
- Total
매일 매일 성장하는 섭섭군
[Seop's 강의노트] 이산신호처리 _ DTFT, 이산시간 푸리에 변환 본문
지금 우리는 ‘푸리에 분석’이라는 도구에 관해서 배우고 있다.
지금까지 연속 주기 신호, 연속 비주기 신호 를 분석하는 CTFS, CTFT를 알아보았다.
이산 비주기 신호에 관하여 알아보도록 하자.
이산 비주기 신호는 연속 비주기 신호를 표본화(Sampling) 하여서 얻어낸 것이다.
표본화 과정은 다음 포스팅때 자세하게 배우겠지만 간단하게 설명해보자면
연속 비주기시 신호 (아날로그 신호)에서 일정 간격으로 주파수 성분과 크기를 뽑아내는 것이다.
흔히 통계에서 전체집단 중 일부를 뽑아내는 것과 같은 개념이라고 볼 수 있다.
그렇다면 연속 비주기 신호를 표본화 하여서 이산 비주기 신호를
얻어냈다면 어떠한 변화가 있을까?
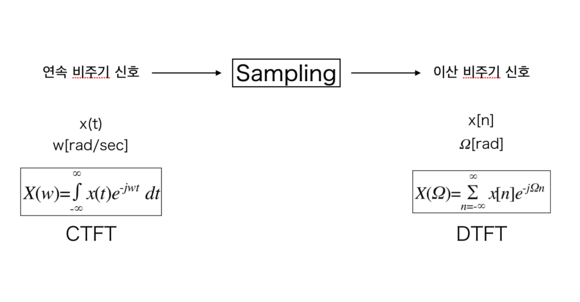
연속 비주기 신호를 샘플링 한 후의 변화이다.
여기서 지켜봐야 할 특징은 시간의 개념이 사라졌다는 것이다.
( [rad/sec]->[rad] & t->n)
여기서 n은 정수이다. 그리고 연속적인 함수가 아니기 때문에 적분을 했던 것에서 합하는 개념으로 바뀌었다.

다음 그림을 보면 이해가 좀 될 것이라 생각이 든다. 이렇게 표본화 과정을 거쳐서 이산 비주기 신호를 만들어 냈고
이를 분석하는 툴이 DTFT이다.
다시한번 말하지만 자세한 표본화 과정은 다음 포스팅에 자세히 다루도록 하겠다.
DTFT를 좀 더 자세하게 바라보면 알 수 있는 특징이 있다.
가장 큰 DTFT의 특징이라고 할 수 있고 중요하다.
바로 주파수 영역에서 주기적으로 반복한다는 것이다.
그 주기는 2Pi 이다.
X(Large Omega) = X(LargeOmega+2Pi)
위 식이 성립한다는 의미이다. 한번 살펴보도록 하자.

다음의 과정을 통해서 DTFT는 주기성을 가지고 있다는 것을 식으로 확인 해 볼 수 있었다.
이것이 말하는 의미는 다음과 같다.
이산신호의 스펙트럼이 유효한 구간은 0< 2Pi 이다.
여기서 좀 더 생각을 해 본다면 주기성을 가지고 있다고 하였으니
0<Pi만 알고있으면 나머지 부분에 관해서는 어떠한 값을 가지고
있는지 알아볼 수 있다는 의미이다.
아직 샘플링에 관해서 제대로 공부를 하지 않았기 때문에 DTFT가
좀 어려울 수 있다.다음 포스팅 때 샘플링에 대해서 이해를 한다면 좀 더
DTFT를 이해를 할 수 있을것이라 생각한다.
'디지털신호처리, DSP' 카테고리의 다른 글
| [Seop's 강의노트] 이산신호처리 _ DTFT의 특징 및 성질 (0) | 2019.10.23 |
|---|---|
| [Seop's 강의노트] 이산신호처리 _ 표본화(Sampling) (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ CTFT, 연속시간 푸리에 변환 (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ CTFS 연속시간 푸리에급수. (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ 푸리에분석 (0) | 2019.10.23 |




