| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- IOS
- 코테준비
- 백준
- 카카오 코딩테스트
- 알고리즘문제풀이
- 릿코드
- 신호처리
- 프로그래머스
- 파이썬
- 스위프트
- 트라이
- SWIFT
- 전자공학
- leet code
- 이산신호처리
- Leet Coding Challenge
- leetcode
- 독서노트
- 알고리즘 문제풀이
- 코딩테스트
- SWIFTUI
- PYTHON
- DSP
- Trie
- 코테
- backjoon
- DTFT
- dft
- 컨볼루션
- 알고리즘
- Today
- Total
매일 매일 성장하는 섭섭군
[Seop's 강의노트] 이산신호처리 _ 복소수 본문
허수를 알고 있는가?
루트 -1 를 흔히 j 또는 i등으로 표시하고 있다.
복소수 영어로 하면 Complex number 직역하자면 복잡한 숫자라는
의미이다. 그도 그럴 만한 것이 제곱에서 음수가 나오는 것은 자연계에서 찾아볼 수 없는 허수를 포함하고 있기 때문이다.
그런데 왜 우리는 복소수 라는 개념을 생각보다 많이 사용하게 될까?
다음 그래프롤 한번 봐 보자.

직교좌표계 상에서 (a,b)라는 점을 표시해 두었다. 우리가 손으로 그릴 때는 손 쉽게 표현이 가능하다.
하지막 하나의 수식으로 표현하기 위해서 복소수가 쓰이게 된다.
위 그래프 상의 점 (a,b)를 식으로 표현하면 z=a+jb 가 된다. 전자공학에서는 i를 전류로 쓰는 경우가 많으므로 j로 표시하도록 하겠다. 여기서 복소수가 붙은 jb 가 허수부가 되면 a가 실수부가 된다.
이렇게 복소수를 사용하여 직교좌표계 위의 한점을 표시할 수 있다.
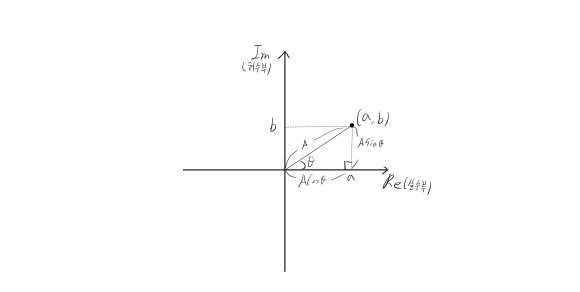
다음 그래프는 각의 개념이 들어 가 있다. 원점에서 (a,b)까지의 거리를 A라고 한다면
a =Acos∅ , b=Asin∅ 가 되게 된다. 식을 다시 써보게 되면
z=Acos∅ + Ajsin∅
이렇게 표시를 할 수 있다. 이를 더 간단히 만들어 볼 수 있다. 오일러의 공식을 사용하면
더욱이 간단하게 쓸 수 있다. 우선 오일러의 공식은 다음과 같이 표시할 수 있다.
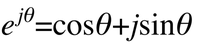
위의 식을 오일러의 공식을 통해서 바꾸어 보자면 다음과 같이 바뀌게 된다.
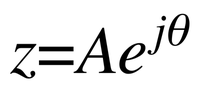
이렇게 복소수와 오일러의 공식을 이용하면 직교좌표 상의 점을 자유롭게 표현 가능하다.
그리고 정현파에 대한 정보도 손 쉽게 알아볼 수 있도록 도움을 준다.
이렇든 사람들이 자연에 존재하지도 않는 허수를 만들고 허수와 실수와 함께 존재하는 복소수를 만든 이유가
우리의 공부를 방해하려고 하는 것이아니다.
우리가 계산을 빠르게 하기 위해서 계산기를 사용하듯 계산기가 없던 시절 더 많은 것을
표현하고 계산하기 위해서 복소수를 만들어낸 것이다.
그러니 나와는 어색하다고 멀리하기 보다는 조금 더 가까이 하고 관찰하다 보면 사용방법을 더 잘 알수 있을 것 같다.
'디지털신호처리, DSP' 카테고리의 다른 글
| [Seop's 강의노트] 이산신호처리 _ DTFT, 이산시간 푸리에 변환 (0) | 2019.10.23 |
|---|---|
| [Seop's 강의노트] 이산신호처리 _ CTFT, 연속시간 푸리에 변환 (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ CTFS 연속시간 푸리에급수. (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ 푸리에분석 (0) | 2019.10.23 |
| [Seop's 강의노트] 이산신호처리 _ 정현파란? (0) | 2019.10.23 |




